1、引言
離子濺射是指載能離子轟擊固體表面,打出離子和中性原子的現象[1]。離子濺射是離子與固體相互作用過程中的重要物理過程之一,在聚變反應堆的壁效應[2]、高能離子推進器、磁控濺射鍍膜[3,4]、濺射離子泵、表面分析、高能離子的收集沉積[5,6]等領域均具有較高的應用價值。在高能離子收集沉積過程,常用的離子加速結構包含金屬絲狀結構,其性能及使用壽命是影響試驗運行穩定性的重要因素,離子的濺射過程會造成金屬絲的表面損失,是影響服役性能及使用壽命的主要因素;因此,對離子濺射過程進行模擬,研究不同合金靶材條件下的離子濺射產額,并基于離子濺射過程對金屬絲壽命進行分析,延長金屬絲結構使用壽命具有重要意義。
目前模擬離子濺射過程中主要有蒙特卡羅方法(MonteCarlo,MC)以及分子動力學方法(moleculardynamics,MD)。常用的基于蒙特卡羅方法進行離子濺射過程模擬的程序為SRIM
(thestoppingandrangofionsinmatter)程序[7],該程序基于1969年Sigmund建立的線性級聯碰撞理論[8],程序中同時包含了大量的實驗修正數據,對于離子入射單質靶材工況適用性強[9,10],由于SRIM在程序計算過程中認為固體靶為非晶靶,入射離子與靶材中原子的相互作用視為二體碰撞過程,未考慮合金晶體結構和多體相互作用問題,SRIM程序的計算結果可能存在較大偏差。
分子動力學方法是按照該體系內部的動力學規律來確定位置和速度隨時間演化的一種模擬方法,通過跟蹤系統中每個粒子的個體運動,給出微觀量(粒子坐標、速度)與宏觀可觀測量(溫度、壓力、比熱、彈性模量等)的關系[11–15],在計算過程中可以充分考慮合金基底中原子相互作用勢,和離子與合金表面多體相互作用[16],更適用于高能離子入射合金靶材的離子濺射過程的計算。
本文基于分子動力學方法,利用LAMMPS(large-scaleatomic/molecularmassivelyparallelsimulator)程序[17,18]對基底材料進行原子晶體尺度建模,建立重離子入射合金靶材初始狀態及持續后入射靶材表面混亂狀態下的離子濺射參數計算模型;在此基礎上研究不同合金不同離子入射角條件下的濺射產額及金屬絲壽命與試驗結果進行了對比,并基于理論模型找到了一種有利于金屬絲服役壽命提升的材料。
2、物理模型及模擬方法
當載能離子入射合金靶材時,會不斷與合金靶材中原子發生碰撞并損失能量,同時靶材中的原子在碰撞中獲得的能量超過其位移能后脫離原來的晶格位置,并與其他原子發生碰撞形成一系列反沖級聯碰撞,當靶材表面的原子獲得的能量超過靶材表面的束縛能后脫離靶材表面形成濺射出射原子。在離子濺射過程中,離子濺射產額定義為每個入射離子引起靶材表面濺射出射原子的數量,濺射產額與入射離子的種類、能量、靶材種類等多種因素相關。
2.1離子濺射產額理論模型
在載能離子轟擊合金靶材的LAMMPS建模模擬過程中,選擇具有周期性邊界、表面取向為(111)的單個晶胞作為計算體系[19],基體溫度選擇為900K,在計算過程中模型域大小的控制、原子間相互作用勢的選取是影響模型復雜度及模型計算準確性的重要因素。
2.1.1模型域和原子間相互作用力
由于離子濺射過程能量作用區域大,入射離子在靶材內發生級聯碰撞的過程中,入射離子能量由晶格間金屬鍵進行高效傳遞,由碰撞引起的能量傳遞距離較遠,而實際上影響碰撞濺射的較高能量傳遞范圍很小。對于濺射中心區域外部的原子層,同時具備吸收能量與反射能量的能力,為了充分反應靶材濺射發展過程的同時降低單原子計算時間,提高計算效率,選取較小的靶材表面高能碰撞區域(24×24×18(lattice))作為中心碰撞區域內層原子進行模擬。同時利用Langevin控溫法[20]在碰撞區域外包裹一層額外的能量吸收反射原子層,以此替代大尺度模型中高能碰撞區域外的原子的方法。圖1為Langevin控溫法模型域劃分示意圖。
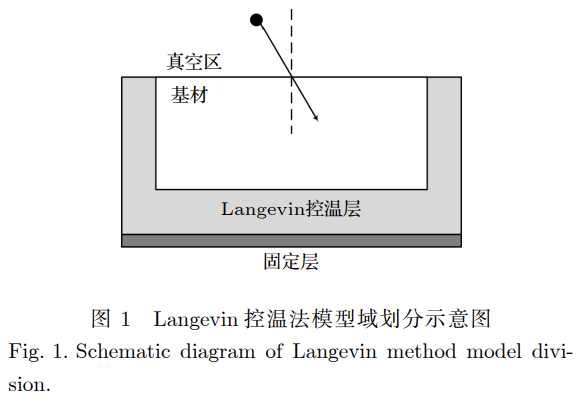
在分子動力學模擬過程中,原子和分子的軌跡是通過數值求解粒子相互作用系統的牛頓運動方程來確定,其中粒子之間的力Fc及勢能通常是通過原子間勢或分子力學力場進行計算,在內層高能原子碰撞區,常用的描述原子間相互作用勢有LJ(Lennard-Jones)勢[21]、EAM(EmbeddedAtomMethod)勢[22]、ZBL(ZieglerBiersackLittmark)勢[23]等,其中LJ勢通常用于描述二體原子之間的相互作用,EAM勢用于描述金屬原子之間的相互作用,ZBL勢更適用于金屬原子的近距離相互作用[23,24],選擇ZBL勢做為原子間相互作用勢函數。
根據Langevin控溫模型公式,在外層Langvein控溫層,在原有原子間作用力Fc基礎上額外增加兩項阻尼力Ff與Fr,以此模擬無限大原子模型對控溫層內部區域的應力吸收與反射:
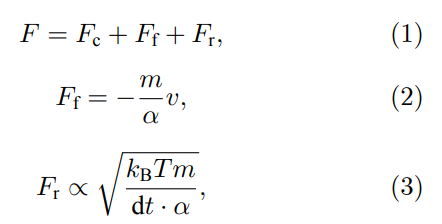
式中,F為控溫區原子所受合力,eV/?;Fc為原子之間基于力場作用的保守力,eV/?;Ff為與粒子速度成正比的摩擦阻力,eV/?;Fr為溫度T下原子與其他粒子隨機碰撞所產生的力,eV/?;m為原子質量,g;v為原子速度,?/ps;α為阻尼系數,ps;kB為玻爾茲曼常數,1。380649×10–23J/K;T為原子溫度,K;dt為計算時間步長,ps。
同時建立近似等價于無窮大基底(40×40×24(lattice))的模型及確定的主要碰撞區域的原子模型,分別選取不同阻尼系數,對其進行相同入射位置、相同入射能量和相同入射角度的濺射模擬,監控在原子入射過程中的平均原子能量變化,當計算模型中碰撞原子能量變化與無窮大基板中碰撞原子能量變化相同或相近時,即認為此時計算模型與無窮大基板等價,當選取的阻尼系數使得內外層碰撞區域的原子能量波動,與近似無窮大基底條件下的原子能量波動在各時間步長內的偏差均≤10%時,此時的阻尼系數α值為所求。
2.2持續入射條件下的離子濺射模型
由于離子引出過程持續時間較長,持續入射一段時間后,靶材表層含有大量的入射離子元素,為提高靶材由初始入射狀態至穩定初始入射狀態的計算效率,對持續入射狀態靶材計算模型進行簡化,借助蒙特卡羅方法,首先利用SRIM程序計算入射離子元素濺射產額為1時穩態條件下,靶材內部入射元素含量和分布隨深度變化的概率密度函數。
同時,靶材經過離子入射后,表層原子的晶格結構被破壞,在經歷足夠多次的濺射后,模擬區域的原子結構逐漸變得混亂,最終達到穩定的混亂狀態,此時即為持續入射狀態下靶材不摻雜離子的原子結構,以此原子結構分布作為基礎,按照入射元素隨深度變化的概率密度分布函數將不同深度原有原子替換為入射元素原子并進行充分弛豫,即可得到近似穩態濺射的靶材原子模型,基于此模型進行穩態條件下的濺射參數計算。
2.3金屬絲壽命計算模型
在高能重離子進行加速、收集的過程中,常見用于離子加速的一種陰極結構為圓形絲狀結構,建立金屬絲服役壽命計算模型,對金屬絲使用壽命進行評估。
在一定的離子入射強度及入射方向下,對于圓形金屬絲,各處的入射仰角(離子入射方向與入射平面法線夾角)均不相同,將圓形金屬絲簡化為不同等分區域內入射仰角相同的多邊形計算。金屬絲的質量及表面損失為離子濺射損失,單位時間各等分區域內截面變化如下:
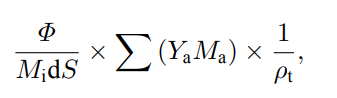
式中,為入射離子通量(s-1.cm-2);為入射原子相對摩爾質量;為靶材所含元素的濺射產額,為靶材所含元素的相對摩爾質量,為靶材密度。
通過計算不同離子入射總量下,各等分區域截面變化情況,得到金屬絲截面隨離子入射總量的變化情況,進而獲得金屬絲壽命。
3、結果及討論
3.1不同合金的濺射產額
3.1.1初始入射狀態下的濺射產額
以銫元素為例,計算了入射離子在能量為9keV入射,不同入射角,316L不銹鋼、625合金作為基底材料的條件下的濺射產額曲線及與SRIM計算結果的對比,結果如圖2所示。
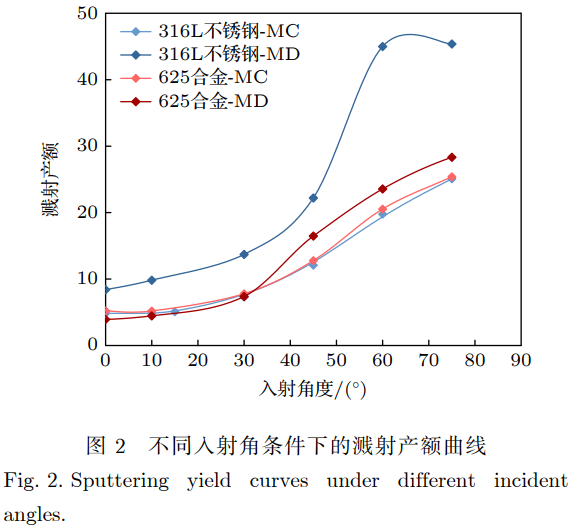
由圖2結果可知,當基底材料為316L不銹鋼時,分子動力學計算的濺射產額結果約為SRIM計算的2倍;當基底材料為625合金時,分子動力學計算的濺射產額結果與SRIM結果相近。對比結果表明,SRIM軟件未在計算中考慮晶格結構對濺射過程的影響,而該影響在濺射產額計算中不可忽略,同時分子動力學計算結果與試驗得到的金屬絲材質為316L不銹鋼時的壽命低于625合金結果相一致,因此后續壽命計算均需要以分子動力學計算結果為基準,SRIM計算結果作為參考。
3.1.2持續入射條件下的濺射產額
根據持續入射條件下的原子模型,以銫元素在在能量為9keV入射316L不銹鋼為例,得到持續入射條件下的不銹鋼內部結構(圖3(b))。
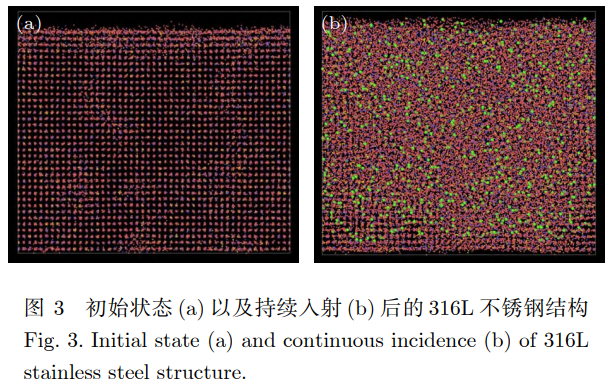
將持續入射后的原子模型及原子間相互作用勢函數代入LAMMPS的計算中得到,不同入射仰角,316L不銹鋼、625合金作為基底材料持續入射的條件下的濺射產額曲線,結果如圖4所示。
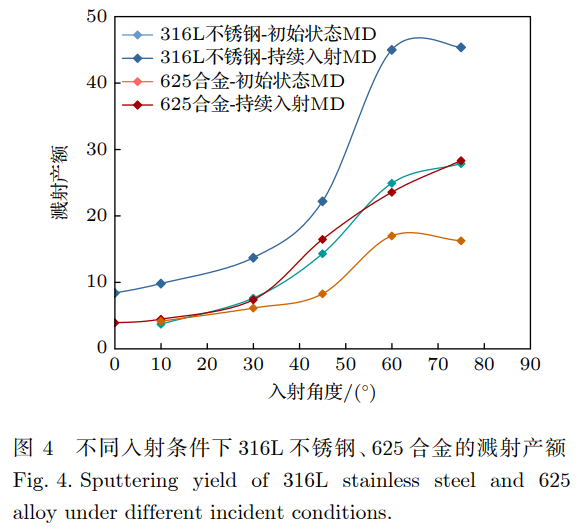
圖4結果表明,在初始狀態下合金靶材具有完整的晶格結構,相鄰晶格原子間在濺射條件下能量傳遞指向性更高,有更大的能量傳遞至靶材表面,因此相比SRIM計算結果,初始狀態靶材分子動力學計算所得濺射產額更大。由于經歷長時間入射后,合金金屬表層晶格被破壞,表層原子排列趨于混亂,因此持續入射后混亂狀態下的濺射產額小于初始狀態濺射產額。由于在625合金中含有8%—10%的鉬元素,部分鉬元素在合金基體中以固溶的形式存在,在強化了合金的同時,給625合金帶來了一部分的晶格畸變,導致部分晶格不完整,使得入射離子的能量在傳遞的過程中更為分散,原子間的約束能力較弱,因此入射能量在合金中的耗散較快,傳遞至表面原子的能量較小,使得濺射產額較小,明顯低于316L不銹鋼的濺射產額。
3.2金屬絲壽命預測與驗證
為確定長時間入射后的金屬絲表面形貌變化對離子濺射參數的影響,對一塊離子長時間持續入射后的金屬平板表面進行了掃描電子顯微鏡(scanning electron microscope,SEM)表面形貌測試,根據電鏡對其表面的觀測結果可知(圖5),宏觀上平整的平板表面并非光滑平面,經過離子入射,表面呈現大小不一的“隕石坑”狀結構。該結構增加了部分粒子的入射角度,提高了實際濺射產額,因此需要評估“隕石坑”結構對實際濺射產額的影響。

根據圖像可知,“隕石坑”結構半徑范圍在10μm級別,而濺射影響區域在100?(1?=10–10m),因此“隕石坑”結構對于金屬絲的濺射行為可視為宏觀幾何結構,隕石坑壁按照斜平面進行計算。建立“隕石坑”形貌模型,近似高斯分布:
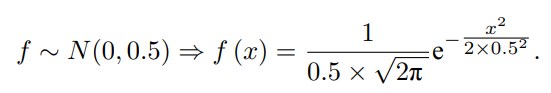
耦合“隕石坑”結構形貌模型,集合離子濺射參數計算模型,依據2.3節中所述金屬絲截面隨時間變化計算模型,以銫元素入射為例,計算得到表1所述入射條件下,金屬絲截面隨離子入射時間變化的結果,如圖6所示。
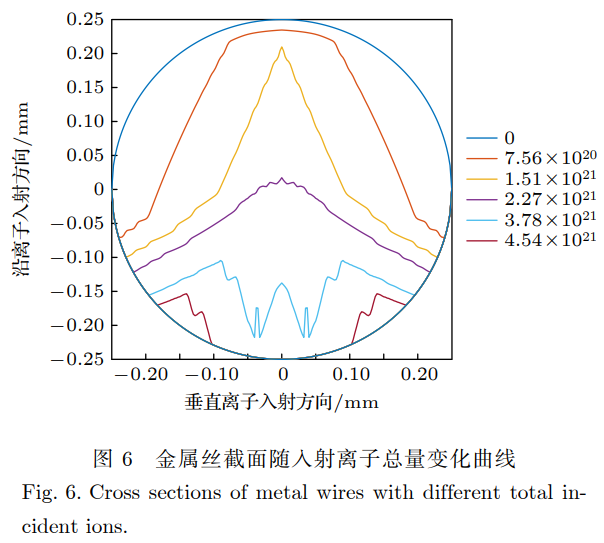
根據圖6結果,金屬絲在入射離子總量達到約3.70×1021時,厚度方向上沿離子入射方向最薄處已降低至0。
05mm以下,此時材料由于離子轟擊所承受的拉力已超過材料能承受的拉力極限,因此認為材料已失效;為驗證理論計算結果的準確性,對在相同入射條件下,離子入射總量約為2.27×1021時的金屬絲截面進行掃描電子顯微鏡表面形貌測試,試驗測得金屬絲截面形貌及尺寸如圖7所示。

根據圖7中結果,將理論計算結果與實際實驗測量相比,寬度方向上誤差為1.84%,厚度方向上誤差約為1。
75%,與理論值相比誤差均<10%,由此驗證了離子濺射為影響金屬絲壽命的主要因素,同時驗證了理論計算模型的準確性及適用性,因此后續采用分子動力學方法進行不同材料的離子濺射過程的模擬,尋找耐濺射材料,優化金屬絲服役壽命。
3.3金屬絲結構壽命提升
根據3.2節中分析,驗證了離子濺射為影響金屬靶材壽命的主要因素,在不改變金屬絲初始直徑條件下,提升金屬靶材壽命的主要方式為金屬絲材料優化,選取濺射產額較小、晶體結構松散、密度較高的材料,可提升金屬絲壽命。經過多種元素計算,評估Ni-Ti合金為面心立方晶體,整體晶體結構較為松散,晶格常數小于625合金,吸收離子動能能力較強,不同入射角條件下在離子持續入射后Ni-Ti合金與625合金相比的濺射產額如圖8所示。
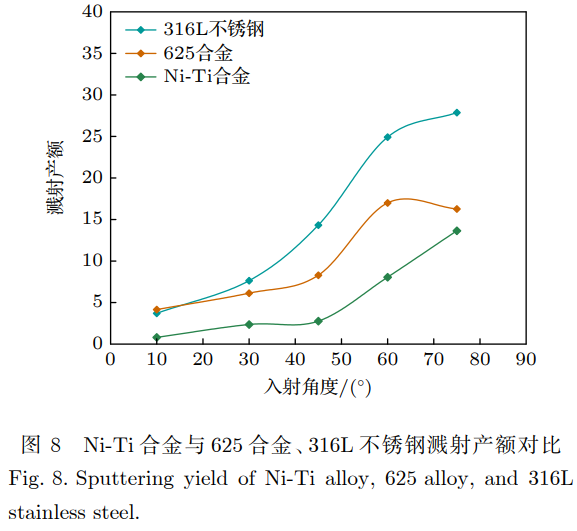
根據圖8所示的結果,相對625合金及316L不銹鋼,不同入射角度下Ni-Ti合金的濺射產額均更小。在Ni-Ti合金材質下,計算得到與3.2節中相同入射條件下,金屬絲截面隨時間的變化曲線如圖9所示。
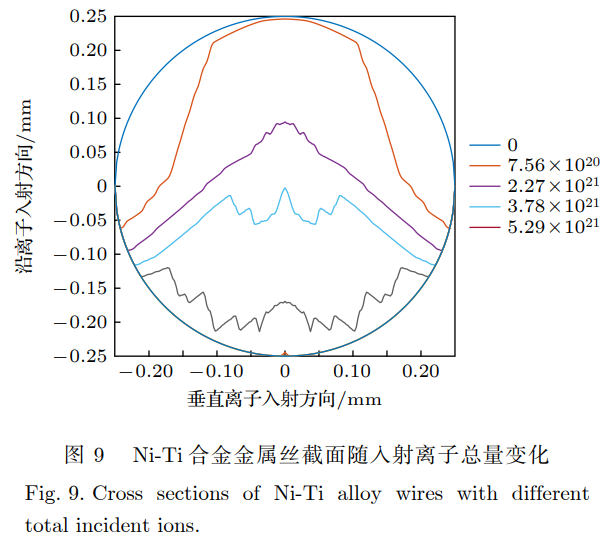
根據圖中結果,金屬絲材質為Ni-Ti合金時,金屬絲失效的入射離子總量可由3.70×1021提升至5.14×1021,在離子束流密度不變的情況下金屬絲壽命可提升約39%,根據計算結果,在后續選材過程中可選取Ni-Ti合金材料,以此降低材料濺射產額,延長金屬絲使用壽命。
4、結論
本文基于載能離子長時間收集沉積過程中,離子濺射過程影響陰極金屬絲服役性能及使用壽命的問題,建立了基于分子動力學及Langevin控溫模型的離子濺射參數計算模型及金屬絲壽命計算模型,并基于模型提出了金屬絲壽命優化方式,主要結論如下。
1)基于分子動力學模型及Langevin控溫模型,利用LAMMPS程序進行了靶材初始條件及離子持續高通量入射條件下下的靶材原子尺度建模,建立了載能重金屬離子入射復雜混合物合金靶材的離子濺射參數計算模型。
2)基于本文建立了濺射產額計算模型計算發現,區別于SRIM軟件計算得到的相同入射條件下,625合金與316L不銹鋼濺射產額相近結果,分子動力學方法計算得到的625合金的濺射產額明顯低于316L不銹鋼,這是由于625合金原子間約束能力較弱,入射能量在合金中耗散較快,傳遞至表面原子的能量較小,使得同一入射角度下,625合金,濺射產額較小,顯著小于不銹鋼的濺射產額。
3)計算得到了在給定入射條件下金屬絲截面隨試驗時間變化的曲線,預測了金屬絲失效時間,并進行了相同入射條件下金屬絲截面與試驗結果的對比,金屬絲寬度及厚度方向上計算結果與試驗結果偏差均小于10%,驗證了理論計算模型的準確性和適用性,對預測不同入射條件下金屬絲使用壽命并進行優化改進具有重要意義。
4)基于本文建立的理論模型,對金屬絲壽命優化提升進行計算,計算結果表明將金屬絲材質由625合金優化為Ni-Ti合金,金屬絲壽命可實現顯著提升,提升比例約39%。
參考文獻
[1]Tian M B, Cui F Z 1987 Physics 17 177 (in Chinese) [田民波,崔福齋 1987 物理 17 177]
Zhang L, Zhang Z L 2006 Journal of Anhui Univ. of Sci. and Tech. 26 69 (in Chinese)
[2][張萊, 張竹林 2006 安徽理工大學學 報 26 69]
Li T J, Cui S H, Liu L L, Li X Y, Wu Z X, Ma Z Y, Fu J Y, Tian X B, Zhu J H, Wu Z Z 2021 Acta Phys. Sin. 70 045202(in Chinese)
[3][李體軍, 崔歲寒, 劉亮亮 李曉淵, 吳忠燦, 馬正永,傅勁裕, 田修波, 朱劍豪, 吳忠振 2021 物理學報70 045202]
[4]Chen C Z, Ma D L, Li Y T, Leng Y X 2021 Acta Phys. Sin.70 180701 (in Chinese)
[陳暢子, 馬東林, 李延濤, 冷永祥 2021物理學報 70 180701]
[5]Zhu H L, Wang D W 2022 Acta Phys. Sin. 51 1338 (in Chinese)
[朱紅蓮, 王德武 2022 物理學報 51 1338]
[6]Xie G F 2008 Acta Phys. Sin. 57 1784 (in Chinese)
[謝國鋒2008 物理學報 57 1784]
[7]Ziegler J F, Ziegler M D, Biersack J P 2008 Nucl Instrum. Meth. B 268 1818
[8]Sigmund P 1969 Phys. Rev. 184 383Shao Q Y, Huo Y K, Chen J X, Wu S M, Pan Z Y 1991 Acta
Phys. Sin. 40 659 (in Chinese)
[9][邵其鋆, 霍裕昆, 陳建新, 吳士 明, 潘正瑛991 物理學報 40 659]
[10] Mahne N, Cekada M, Panjan M 2022 Coatings 12 1541
[11]Fan K Q, Jia J Y 2005 Micronanoelectr. Tech. 42 133 (in Chinese)
[樊康旗, 賈建援 2005 微納電子技術 42 133]
[12]Lu H F, Zhang C, Zhang Q Y 2003 Nucl. Instrum. Meth. B206 22
[13]Pastewka L, Salzer R, Graff A 2009 Nucl. Instrum. Meth. B267 3072
[14]Jr M F R, Maazouz M, Giannuzzi L A 2008 Appl. Surf. Sci.255 828
[15]Feil H, Zwol J, Zwart S T, Dieleman J 1991 Phys. Rev. B 4313695
[16]Lopez-Cazalilla A, Cupak C, Fellinger M 2022 Phys. Rev. Mate. 6 075402
[17] Plimpton S 1995 J. Comput. Phys. 117 1
[18] Tran H, Chew H B 2023 Carbon 205 180
[19]Yan C, Duan J H, He X D 2011 Acta Phys. Sin. 60 088301(in Chinese)
[顏超, 段軍紅, 何興道 2011 物理學報 60 088301]
[20] Nosé S 1984 J. Chem. Phys. 81 511
[21] Slavinskaya N A 1998 Matem. Mod. 34 3
[22] Daw M S, Foiles S M, Baskes M I 1993 Mater. Sci. Rep. 9 251
[23]Ziegler J F 1988 Ion Implantation Technology (Berlin, Heidelberg: Springer) pp122–156
[24]Yan C, Huang L L, He X D 2014 Acta Phys. Sin. 63 126801(in Chinese)
[顏超, 黃莉莉, 何興道 2014 物理學報 63 126801]
相關鏈接